Центральный угол AOB опирается на хорду АВ длиной 5. При этом угол ОАВ равен 60°. Найдите радиус окружности.
Рассмотрим треугольник АОВ. АО=ОВ, т.к. это радиусы окружности. Следовательно, треугольник АОВ - равнобедренный. Следовательно, /ОВА = /ОАВ = 60° (по свойству равнобедренного треугольника). Заметим, что /АОВ тоже равен 60° (по теореме о сумме углов треугольника). 180°-60°-60°=60°. Следовательно треугольник АОВ - равносторонний (по свойству равностороннего треугольника). Следовательно, ОВ=ОА=АВ=5. Ответ: АВ=5.
Поделитесь решением
Присоединяйтесь к нам...
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=7, DK=14, BC=10. Найдите AD.
Стороны AC, AB, BC треугольника ABC равны 3√
Площадь круга равна 88. Найдите площадь сектора этого круга, центральный угол которого равен 45°.
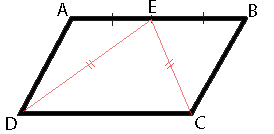В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм - прямоугольник.
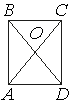Диагонали AC и BD прямоугольника ABCD пересекаются
в точке O, BO=37, AB=56. Найдите AC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: