В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 30°. Найдите величину угла OAB.
Рассмотрим треугольник COD. Этот треугольник
равнобедренный, т.к. ОC и ОD - радиусы, поэтому они равны.
По
свойству равнобедренного треугольника /OCD=/ODC.
Рассмотрим треугольники АОВ и COD. /DOC=/AOB, т.к. они
вертикальные. СО=DO=OB=OA, т.к. это радиусы окружности.
Следовательно, треугольники АОВ и COD равны (по
первому признаку). Поэтому /OBA=/OAB=/ODC=/OCD=30°
Ответ: /OAB=30°.
Поделитесь решением
Присоединяйтесь к нам...
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 31.
Синус острого угла A треугольника ABC равен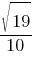 
. Найдите CosA.
Лестница соединяет точки A и B и состоит из 15 ступеней. Высота каждой ступени равна 28 см, а длина – 96 см. Найдите расстояние между точками A и B (в метрах).
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 31 и 32, касаются сторон угла с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=11, а расстояние от точки K до стороны AB равно 3.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: