
 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
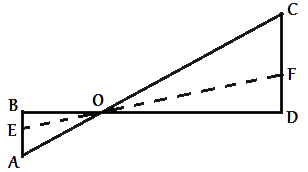 Рисунок,предложенный в задаче можно условно перерисовать в виде треугольников. Рассмотрим треугольники ABO и COD.
Рисунок,предложенный в задаче можно условно перерисовать в виде треугольников. Рассмотрим треугольники ABO и COD.
1) /BOA=/DOC, т.к. они
вертикальные.
2) /OBA=/ODC=90°
3) /BAO=/DCO, т.к. они
внутренние накрест-лежащие.
Следовательно, треугольники ABO и COD
подобны (по признаку подобия). Отсюда следует, что CO/AO=CD/AB. Поэтому при движении, высота концов журавля будет подчиняться этой же пропорции.
CO/AO=CD/AB=CF/AE
4/3=CF/1,5 => CF=4*1,5/3=2.
Ответ: конец длинного плеча опустится на 2 метра.
Поделитесь решением
Присоединяйтесь к нам...
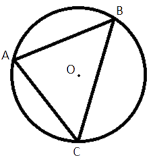 Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:4:11. Найдите радиус окружности, если меньшая из сторон равна 14.
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:4:11. Найдите радиус окружности, если меньшая из сторон равна 14.
Сколько досок длиной 3,5 м, шириной 20 см и толщиной 10 мм выйдет из бруса длиной 140 дм, имеющего в сечении прямоугольник размером 50 см × 60 см?
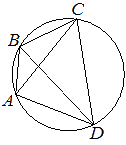 Четырёхугольник ABCD вписан в окружность. Угол ABC равен 138°, угол CAD равен 83°. Найдите угол ABD. Ответ дайте в градусах.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 138°, угол CAD равен 83°. Найдите угол ABD. Ответ дайте в градусах.
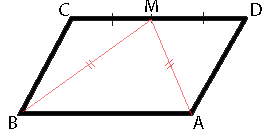 В параллелограмме ABCD точка M — середина стороны CD. Известно, что MA=MB. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме ABCD точка M — середина стороны CD. Известно, что MA=MB. Докажите, что данный параллелограмм — прямоугольник.
 Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 7.
Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 7.
Комментарии: