Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны.
2) В любой треугольник можно вписать окружность.
3) Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.
Рассмотрим каждое утверждение.
1) "Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны", это утверждение верно по
свойствам углов.
2) "В любой треугольник можно вписать окружность", это утверждение верно по свойству вписанной окружности.
3) "Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом". По
свойству параллелограмма, противоположные стороны попарно равны. А раз смежные стороны равны, то и противоположные им стороны так же равны. Таким образом получается, что все четыре стороны такого параллелограмма равны. А это и есть
определение ромба.
Поделитесь решением
Присоединяйтесь к нам...
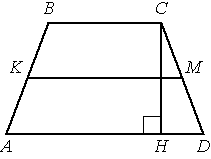В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 10, а меньшее основание BC равно 4.
Имеются два сосуда, содержащие 12 кг и 8 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 65% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60% кислоты. Сколько килограммов кислоты содержится во втором растворе?
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника BKP к площади треугольника AMK.
Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=13.
Периметр квадрата равен 184. Найдите площадь квадрата.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: