Какие из данных утверждений верны? Запишите их номера.
1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
2) Площадь круга меньше квадрата длины его диаметра.
3) Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник — ромб.
Рассмотрим каждое утверждение.
1) "Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны", это утверждение неверно, т.к. не соответствует ни одному из
признаков равенства треугольников.
2) "Площадь круга меньше квадрата длины его диаметра". Прощадь круга равна ΠR2, или ΠD2/4. Число Π (Пи) равно, приблизительно, 3,14. Тогда Sкруга=0,785D2. А это, конечно меньше, чем D2. Утверждение верно
3) "Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник — ромб", это утверждение неверно, т.к. полностью не соответствует ни одному
свойству ромба.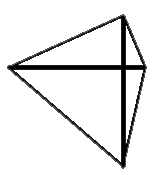
Например, четырехугольник, изображенный на рисунке, его диагонали перпендикулярны, но очевидно, что это не ромб.
Поделитесь решением
Присоединяйтесь к нам...
В трапеции ABCD AB=CD, ∠BDA=49° и ∠BDC=13°. Найдите угол ABD. Ответ дайте в градусах.
Прямые m и n параллельны. Найдите ∠3, если ∠1=22°, ∠2=72°. Ответ дайте в градусах.
Найдите площадь треугольника, изображённого на рисунке.
На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
Укажите номера верных утверждений.
1) Существует квадрат, который не является прямоугольником.
2) Если два угла треугольника равны, то равны и противолежащие им стороны.
3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: