
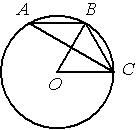
 Точка О – центр окружности, /BOC=60° (см. рисунок). Найдите величину угла BAC (в градусах).
Точка О – центр окружности, /BOC=60° (см. рисунок). Найдите величину угла BAC (в градусах).
По условию /BOC=60°, этот угол является
центральным, соответственно дуга ВC тоже равна 60°. /BAC - является
вписанным углом и равен половине дуги, на которую опирается (по теореме о вписанном угле). Соответственно, 60/2=30.
Ответ: /BAC=30°.
Поделитесь решением
Присоединяйтесь к нам...
 Картинка имеет форму прямоугольника со сторонами 24 см и 37 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 1440 см2. Какова ширина окантовки? Ответ дайте в сантиметрах.
Картинка имеет форму прямоугольника со сторонами 24 см и 37 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 1440 см2. Какова ширина окантовки? Ответ дайте в сантиметрах.
 На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 1 м, высота фонаря 9 м?
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 1 м, высота фонаря 9 м?
 В треугольнике два угла равны 72° и 42°. Найдите его третий угол. Ответ дайте в градусах.
В треугольнике два угла равны 72° и 42°. Найдите его третий угол. Ответ дайте в градусах.
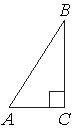 В треугольнике ABC угол C равен 90°, sinB=3/5, AB=10. Найдите AC.
В треугольнике ABC угол C равен 90°, sinB=3/5, AB=10. Найдите AC.
 На стороне AB треугольника ABC взята такая точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=40, BC=45 и CD=24.
На стороне AB треугольника ABC взята такая точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=40, BC=45 и CD=24.
Комментарии: