Точка О – центр окружности, /BOC=110° (см. рисунок). Найдите величину угла BAC (в градусах).
По условию /BOC=110°, этот угол является
центральным, соответственно дуга ВC тоже равна 110°. /BAC - является
вписанным углом и равен половине дуги, на которую опирается (по теореме о вписанном угле). Соответственно, 110/2=55.
Ответ: /BAC=55°.
Поделитесь решением
Присоединяйтесь к нам...
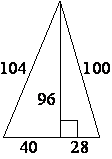Найдите площадь треугольника, изображённого на рисунке.
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 9 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=9, AC=18, MN=8. Найдите AM.
В треугольнике ABC угол C равен 90°, BC=3, AB=5. Найдите cosB.
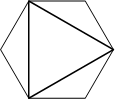Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: