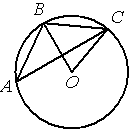
Точка О – центр окружности, /BAC=20° (см. рисунок). Найдите величину угла BOC (в градусах).
По условию /BAC=20°, этот угол является
вписанным углом и равен половине градусной меры дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, градусная мера дуги, в нашей задаче, равна 20°*2=40°.
/BOC является
центральным и равен градусной мере дуги, на которую опирается, следовательно, /BOC=40°.
Ответ: /BOC=40°.
Поделитесь решением
Присоединяйтесь к нам...
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника AMK.
В окружности с центром в точке О проведены диаметры AD и BC, угол
OAB равен 65°. Найдите величину угла OCD.
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=24, BC=18. Найдите AD.
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=5, AC=45.
Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: