Сторона ромба равна 24, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
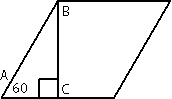Рассмотрим треугольник АВС, этот треугольник
прямоугольный (по условию задачи). /A=60°, следовательно по
теореме о сумме углов треугольника /АВС = 180°-90°-60°=30°. По
свойству прямоугольного треугольника АС=АВ/2=24/2=12. Следовательно вторая половина стороны ромба = 24-12=12. Т.е., в данной задаче, высота, проведенная к стороне ромба делит эту сторону на две равные части.
Ответ: длины обоих отрезков равны 12.
Поделитесь решением
Присоединяйтесь к нам...
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
Лестница соединяет точки A и B. Высота каждой ступени равна 10,5 см, а длина – 36 см. Расстояние между точками A и B составляет 15 м. Найдите высоту, на которую поднимается лестница (в метрах).
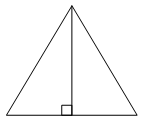Высота равностороннего треугольника равна 15√
Высота BH ромба ABCD делит его сторону AD на отрезки AH=4 и HD=1. Найдите площадь ромба.
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 45 и 46, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: