
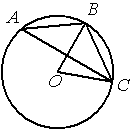
 Точка О – центр окружности, /BOC=70° (см. рисунок). Найдите величину угла BAC (в градусах).
Точка О – центр окружности, /BOC=70° (см. рисунок). Найдите величину угла BAC (в градусах).
По условию /BOC=70°, этот угол является
центральным, соответственно дуга ВC тоже равна 70°. /BAC - является
вписанным углом и равен половине дуги, на которую опирается (по теореме о вписанном угле). Соответственно, 70/2=35.
Ответ: /BAC=35°.
Поделитесь решением
Присоединяйтесь к нам...
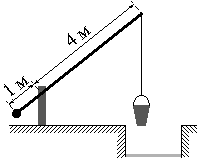 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 1 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 1 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
 На отрезке AB выбрана точка C так, что AC=60 и BC=27. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
На отрезке AB выбрана точка C так, что AC=60 и BC=27. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что /NBA=38°. Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что /NBA=38°. Найдите угол NMB. Ответ дайте в градусах.
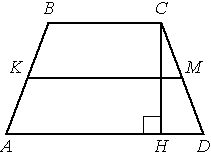 В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 6.
В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 6.
 Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=28. Диагональ параллелограмма BD равна 53. Найдите площадь параллелограмма.
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=28. Диагональ параллелограмма BD равна 53. Найдите площадь параллелограмма.
Комментарии: