
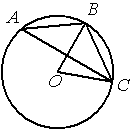
 Точка О – центр окружности, /BOC=70° (см. рисунок). Найдите величину угла BAC (в градусах).
Точка О – центр окружности, /BOC=70° (см. рисунок). Найдите величину угла BAC (в градусах).
По условию /BOC=70°, этот угол является
центральным, соответственно дуга ВC тоже равна 70°. /BAC - является
вписанным углом и равен половине дуги, на которую опирается (по теореме о вписанном угле). Соответственно, 70/2=35.
Ответ: /BAC=35°.
Поделитесь решением
Присоединяйтесь к нам...
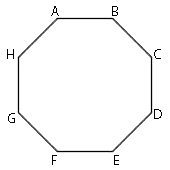 ABCDEFGH – правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
ABCDEFGH – правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
 Найдите площадь квадрата, описанного около окружности радиуса 32.
Найдите площадь квадрата, описанного около окружности радиуса 32.
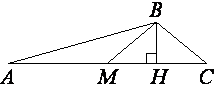 В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=216, HC=54 и ∠ACB=40°. Найдите угол AMB. Ответ дайте в градусах.
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=216, HC=54 и ∠ACB=40°. Найдите угол AMB. Ответ дайте в градусах.
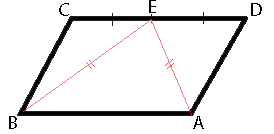 В параллелограмме ABCD точка E — середина стороны CD. Известно, что EA=EB. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме ABCD точка E — середина стороны CD. Известно, что EA=EB. Докажите, что данный параллелограмм — прямоугольник.
 В треугольнике ABC проведена биссектриса AL, угол ALC равен 169°, угол ABC равен 160°. Найдите угол ACB. Ответ дайте в градусах.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 169°, угол ABC равен 160°. Найдите угол ACB. Ответ дайте в градусах.
Комментарии: