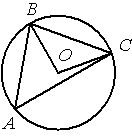
Точка О – центр окружности, /BOC=100° (см. рисунок). Найдите величину угла BAC (в градусах).
По условию /BOC=100°, этот угол является
центральным, соответственно дуга ВC (верхняя часть) тоже равна 100°. /BAC - является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле). Соответственно, 100/2=50.
Ответ: /BAC=50°.
Поделитесь решением
Присоединяйтесь к нам...
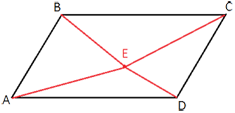Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
Площадь прямоугольного треугольника равна 968√
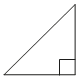В прямоугольном треугольнике гипотенуза равна 82, а один из острых углов равен 45°. Найдите площадь треугольника.
Какие из данных утверждений верны? Запишите их номера.
1) Вокруг любого треугольника можно описать окружность.
2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
3) Площадь трапеции равна произведению средней линии на высоту.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади четырехугольника KPCM к площади треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: