ОГЭ, Математика. Геометрия: Задача №656C84 | Ответ-Готов

Юмор

Автор: Таська
Так выглядит современная программа обучения.
�...читать далее

ОГЭ, Математика.
Геометрия: Задача №656C84

Задача №633 из 1087
Условие задачи:

Площадь прямоугольного треугольника равна 968√3/3. Один из острых углов равен 60°. Найдите длину катета, лежащего напротив этого угла.

Решение задачи:

Обозначим:
a - искомый катет
b - второй катет
c - гипотенуза
sin60°=√3/2 ( табличное значение)
sin60°=a/c=√3/2 (по определению синуса)
c=2a/√3
По теореме Пифагора:
a²+b²=c²
a²+b²=(2a/√3)²
a²+b²=4a²/3
3(a²+b²)=4a²
3a²+3b²=4a²
3b²=a²
b²=a²/3
b=a/√3
Из условия: S_{треугольника}=ab/2=968√3/3
a*(a/√3)/2=968√3/3
a²/√3=1936√3/3
a²=√3*1936√3/3
a²=1936(√3)²/3
a²=1936
a=44
Ответ: a=44

Поделитесь решением

Присоединяйтесь к нам...

Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас'

Другие задачи из этого раздела

Задача №EE59B5

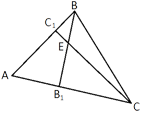Высоты BB₁ и CC₁ остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы BB₁C₁ и BCC₁ равны.

Задача №02270F

Найдите площадь треугольника, изображённого на рисунке.

Задача №3B4B4B

В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 136. Найдите стороны треугольника ABC.

Задача №C6A628

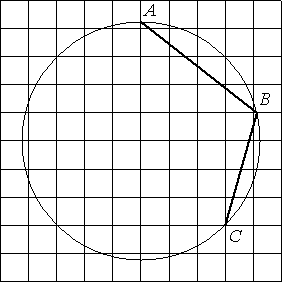Найдите угол ABC. Ответ дайте в градусах.

Задача №17DF0C

Радиус вписанной в квадрат окружности равен 14√2. Найдите диагональ этого квадрата.

Комментарии:

Найти задачу

Подписаться на новости сайта

Хочу получать новые решения

email рассылки Ни какого спама

email рассылки

X

Значение не введено

X

Copyright otvet-gotov.ru 2014-2021. Все права защищены.