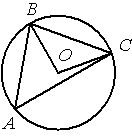
Точка О – центр окружности, /BOC=100° (см. рисунок). Найдите величину угла BAC (в градусах).
По условию /BOC=100°, этот угол является
центральным, соответственно дуга ВC (верхняя часть) тоже равна 100°. /BAC - является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле). Соответственно, 100/2=50.
Ответ: /BAC=50°.
Поделитесь решением
Присоединяйтесь к нам...
Площадь прямоугольного треугольника равна 18√
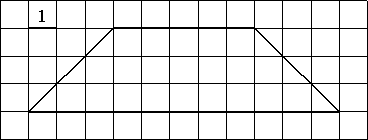Найдите площадь трапеции, изображённой на рисунке.
В треугольнике ABC AB=BC=37, AC=24. Найдите длину медианы BM.
Лестница соединяет точки A и B. Высота каждой ступени равна 10,5 см, а длина – 36 см. Расстояние между точками A и B составляет 15 м. Найдите высоту, на которую поднимается лестница (в метрах).
Основания BC и AD трапеции ABCD равны соответственно 4 и 64, BD=16. Докажите, что треугольники CBD и ADB подобны.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: