На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,6 м, если длина его тени равна 2 м, высота фонаря 4 м?
Перерисуем данный рисунок в виде треугольников и обозначим интересующие нас точки.
Рассмотрим треугольники ABC и DCE:
∠C - общий
∠B=∠DEC=90°
Тогда, по первому признаку данные треугольники подобны.
Следовательно, мы можем записать пропорцию:
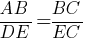
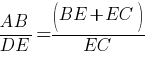
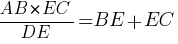
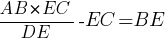
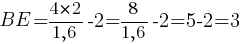
Ответ: 3
Поделитесь решением
Присоединяйтесь к нам...
Площадь прямоугольного треугольника равна 50√
Найдите тангенс угла
AOB.
В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=3 и CH=1. Найдите cosB.
Точка O – центр окружности, на которой лежат точки P, Q и R таким образом, что OPQR – ромб. Найдите угол ORQ. Ответ дайте в градусах.
В треугольнике ABC угол C равен 90°, sinA=0,4, AC=√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-11-26 20:46:55) Администратор: Дарья, я доработал немного решение, чтобы стало все понятно и очевидно.
(2017-11-24 16:31:52) Дарья: Как могло получится в ответе 3,если 1,6-2 в результате получится отрицательное число?