Сторона ромба равна 38, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
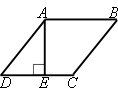150° - это тупой угол, т.е. это ∠DAB и ∠BCD (эти углы равны по
свойству параллелограмма и ромба).
AB||CD (по определению параллелограмма и ромба).
Тогда:
∠DEA=∠BAE=90° (это
накрест лежащие углы).
Следовательно:
∠DAE=∠DAB-∠EAB=150°-90°=60°
Треугольник DAE - прямоугольный, тогда, по определению косинуса:
cos∠EAB=AE/AD
cos60°=AE/38
1/2=AE/38 (по таблице косинусов)
AE=38/2=19 - это и есть
высота.
Ответ: 19
Поделитесь решением
Присоединяйтесь к нам...
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=15, AC=25.
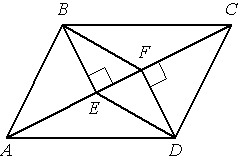В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что ВFDЕ — параллелограмм.
Центральный угол AOB опирается на хорду АВ длиной 6. При этом угол ОАВ равен 60°. Найдите радиус окружности.
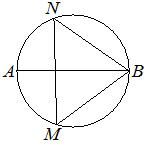На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=36°. Найдите угол NMB. Ответ дайте в градусах.
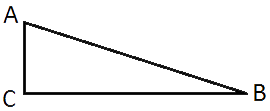Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 40 и 85.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2023-12-19 12:31:20) Fdggf: Fezzxc!???