Какие из данных утверждений верны? Запишите их номера.
1) У равнобедренного треугольника есть ось симметрии.
2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
3) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
Рассмотрим каждое утверждение.
1) "У
равнобедренного треугольника есть ось симметрии", это утверждение верно, ось совпадает с
высотой, опущенной к основанию треугольника.
2) "Если в
параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат", это утверждение верно, т.к. оно совпадает со
свойством квадрата.
3) "Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности", это утверждение неверно, окружности не будут пересекаться, если, например, центры окружностей совпадают.
Поделитесь решением
Присоединяйтесь к нам...
Основание AC равнобедренного треугольника ABC равно 6. Окружность радиуса 4,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Какие из следующих утверждений верны?
1) Средняя линия трапеции равна сумме её оснований.
2) Диагонали ромба перпендикулярны.
3) Площадь треугольника меньше произведения двух его сторон.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 36.
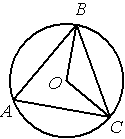Точка О – центр окружности, /BAC=60° (см. рисунок). Найдите величину угла BOC (в градусах).
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=21, BF=20.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: