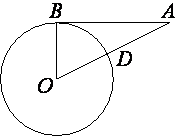
Отрезок AB=32 касается окружности радиуса 24 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
Отрезок AB перпендикулярен OB (по
свойству касательной).
Следовательно, треугольник ABO
прямоугольный.
Тогда можно применить
теорему Пифагора:
AO2=AB2+OB2
AO2=322+242
AO2=1024+576
AO2=1600
AO=40
AO=AD+OD
OD - радиус окружности, следовательно OD=24.
40=AD+24
AD=16
Ответ: 16
Поделитесь решением
Присоединяйтесь к нам...
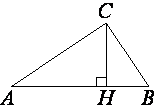В прямоугольном треугольнике ABC катет AC=65, а высота CH, опущенная на гипотенузу, равна 13√
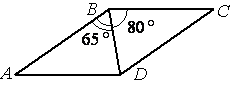Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 80°. Найдите меньший угол параллелограмма.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АС, если сторона АВ равна 4.
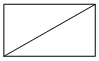В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
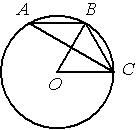Точка О – центр окружности, /BOC=60° (см. рисунок). Найдите величину угла BAC (в градусах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: