
 Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 7.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 7.
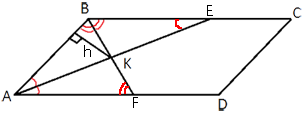 Обозначим точки пересечения
биссектрис со сторонами как показано на рисунке.
Обозначим точки пересечения
биссектрис со сторонами как показано на рисунке.
∠FAK=∠BEK (т.к. это
накрест-лежащие углы).
Получается, что ∠BAK=∠BEK, следовательно треугольник ABE -
равнобедренный (по
свойству равнобедренного треугольника).
Тогда AB=BE.
Треугольники ABK и EBK равны по
первому признаку равенства треугольников.
Следовательно и
высоты у этих треугольников тоже равны.
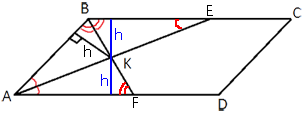 Аналогично, равны и треугольники ABK и AFK.
Аналогично, равны и треугольники ABK и AFK.
Получается, что высота
параллелограмма равна 2h.
Площадь
параллелограмма равна SABCD=2h*BC=2*7*19=266
Ответ: 266
Поделитесь решением
Присоединяйтесь к нам...
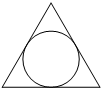 Радиус окружности, вписанной в равносторонний треугольник, равен 2√
Радиус окружности, вписанной в равносторонний треугольник, равен 2√
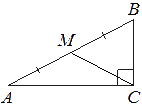 В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=20, BC=10. Найдите CM.
В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=20, BC=10. Найдите CM.
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=3 и MB=12. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=3 и MB=12. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
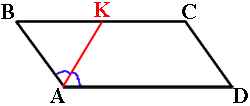 Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=6, CK=10.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=6, CK=10.
 Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Комментарии:
(2017-05-29 00:01:54) Администратор: Нина, к сожалению, у меня нет такой информации.
(2017-05-24 03:23:20) нина: задача из какой части
(2015-05-06 22:00:08) Алексей : Спасибо огромное, понятное дело вы думаете что задачи легкие, но для нашей не полностью сложившейся головы они трудные. Так что спс браток, ваще выручил. Молодчик.