Постройте график функции
y=|x2-x-2|.
Какое наибольшее число общих точек может иметь график данной функции с прямой, параллельной оси абсцисс?
Построить график функции, которая заключена в
модуль, довольно просто.
Достаточно построить график функции без модуля, а потом, всю часть графика, которая располагается под осью Х зеркально отобразить над осью Х. Так и поступим.
Построим график функции y=x2-x-2.
Найдем точки, где график пересекает ось Х, это будут корни уравнения:
x2-x-2=0.
Найдем корни этого квадратного уравнения через дискриминант:
D=(-1)2-4*1*(-2)=1+8=9
x1=(-(-1)+3)/(2*1)=(1+3)/2=2
x2=(-(-1)-3)/(2*1)=(1-3)/2=-1
Теперь найдем координаты вершины параболы:
x0=-b/(2a)=-(-1)/(2*1)=1/2=0,5
y0=0,52-0,5-2=0,25-0,5-2=-2,25
Строим график:
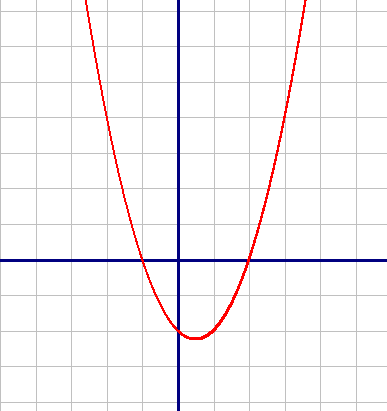
А теперь, как говорилось ранее, часть графика, которая находится под осью Х, зеркально отобразим над осью Х:
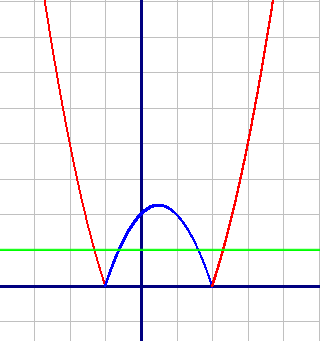
Это и будет графиком функции y=|x2-x-2|.
Очевидно, что график данной функции имеет 4 общие точки с прямой, параллельной оси абсцисс (зеленая прямая).
Ответ: 4
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции
y=3|x+7|-x2-13x-42.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Постройте график функции
x2-10x+25, если x≥4,
x-3, если x<4,
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
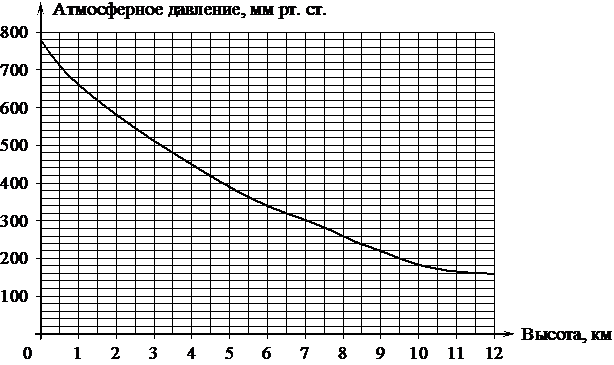На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). Найдите, чему равно атмосферное давление на высоте 7,5 км. Ответ дайте в миллиметрах ртутного столба.
Постройте график функции
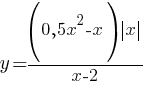
Определите, при каких значениях m прямая y=m не имеет с графиком
ни одной общей точки.
Постройте график функции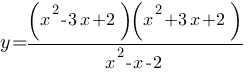 
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Хочу получать новые решения
Ни какого спама
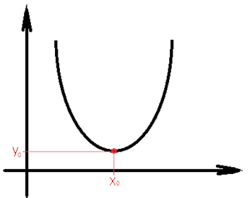Координаты вершины параболы y=ax2+bx+c можно найти по вормулам: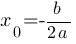
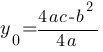
Автор: Таська
Комментарии: