Постройте график функции
x2-6x+11 при x≥2
x+1 при x<2
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Чтобы построить график этой функции, надо построить график каждой подфункции на указанных для подфункций диапазонах.
y1=x2-6x+11 на диапазоне [2;+∞)
y2=x+1 на диапазоне (-∞;2)
Проанализируем графики.
Первая подфункция:
1) график - парабола
2) так как коэффициент а=1 (т.е. больше нуля), то ветви направлены вверх
3) Найдем корни соответствующего уравнения через
дискриминант x2-6x+11=0, чтобы узнать в каких точках парабола пересекает ось Х:
D=(-6)2-4*1*11=36-44=-8
D<0, это означает, уравнение не имеет корней, а значит парабола не пересекает ось Х.
Дальше будем строить по точкам (красный график):
| X | 2 | 3 | 4 | 5 |
| Y | 3 | 2 | 3 | 6 |
| X | 2 | 1 | 0 |
| Y | 3 | 2 | 1 |
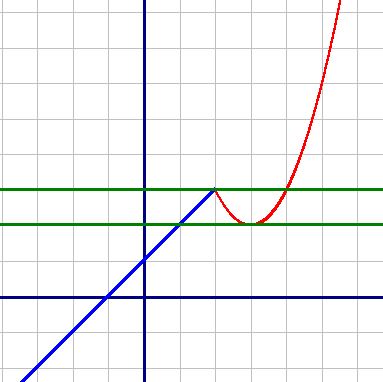y=m - это прямые, параллельные оси Х. Зеленым цветом построены прямые y=m. Очевидно, что только две прямые будут иметь только 2 общие точки с нашим графиком - это прямая, проходящая через точку "излома" графика, и прямая, касающаяся вершины параболы.Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции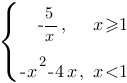 
и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
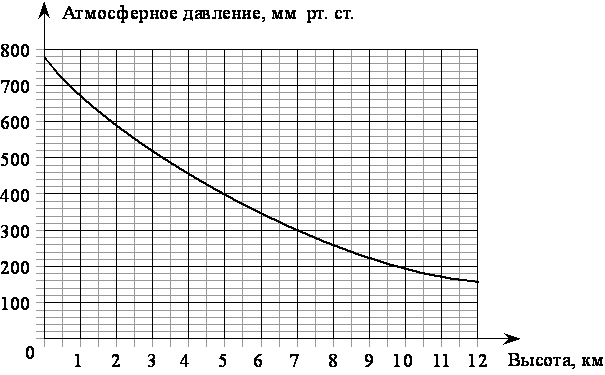На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 720 миллиметров ртутного столба?
Постройте график функции y=x2-|4x+3| и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
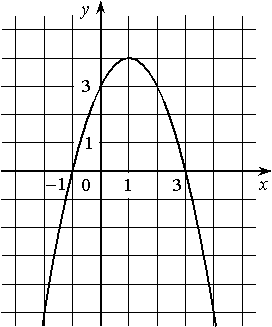На рисунке изображён график квадратичной функции y=ƒ(x).
Какие из следующих утверждений о данной функции являются верными? Запишите их номера.
1) Наибольшее значение функции равно 3
2) Функция убывает на промежутке (-∞;1]
3) ƒ(x)>0 при -1<x<3
Постройте график функции y=|x|(x+1)-6x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Хочу получать новые решения
Ни какого спама
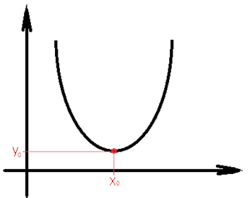Координаты вершины параболы y=ax2+bx+c можно найти по вормулам: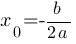
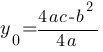
Автор: Таська
Комментарии: