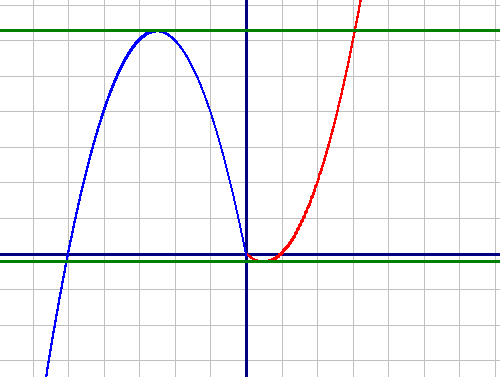
Постройте график функции
y=x|x|+2|x|-3x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Данная функция содержит
модуль, следовательно ее нужно разложить на две функции:
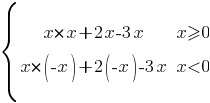
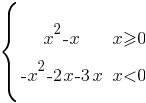
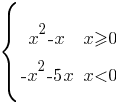
Обе подфункции - параболы. Построим их по точкам:
y1=x2-x на диапазоне от 0 до плюс бесконечности (красный график):
| X | 0 | 1 | 2 | 3 |
| Y | 0 | 0 | 2 | 6 |
| X | 0 | -1 | -2 | -3 |
| Y | 0 | 4 | 6 | 6 |
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции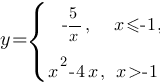 
и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
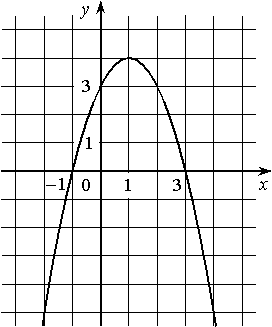На рисунке изображён график квадратичной функции y=ƒ(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) ƒ(x)<0 при x<1
2) Наибольшее значение функции равно 3
3) ƒ(0)>ƒ(4)
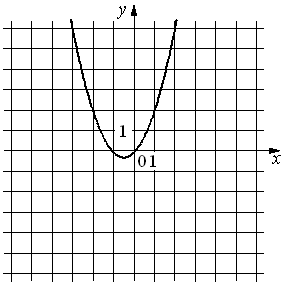На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
| УТВЕРЖДЕНИЯ | ПРОМЕЖУТКИ |
| А) Функция возрастает на промежутке Б) Функция убывает на промежутке |
1) [-3;3] 2) [0;3] 3) [-3;-1] 4) [-3;0] |
Постройте график функции
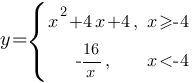
и определите, при каких значениях m прямая y=m имеет с графиком одну или две общие точки.
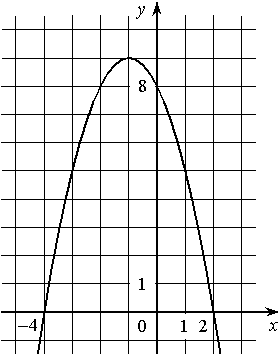На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Функция возрастает на промежутке (-∞;-1]
2) Наибольшее значение функции равно 8
3) f(-4)≠f(2)
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: