ОГЭ, Математика.
Функции: Задача №D28F33

Задача №224 из 287
Условие задачи:

Постройте график функции
y=|x²-x-2|.
Какое наибольшее число общих точек может иметь график данной функции с прямой, параллельной оси абсцисс?

Решение задачи:

Построить график функции, которая заключена в модуль, довольно просто.
Достаточно построить график функции без модуля, а потом, всю часть графика, которая располагается под осью Х зеркально отобразить над осью Х. Так и поступим.
Построим график функции y=x²-x-2.
Найдем точки, где график пересекает ось Х, это будут корни уравнения:
x²-x-2=0.
Найдем корни этого квадратного уравнения через дискриминант:
D=(-1)²-4*1*(-2)=1+8=9
x₁=(-(-1)+3)/(2*1)=(1+3)/2=2
x₂=(-(-1)-3)/(2*1)=(1-3)/2=-1
Теперь найдем координаты вершины параболы:
x₀=-b/(2a)=-(-1)/(2*1)=1/2=0,5
y₀=0,5²-0,5-2=0,25-0,5-2=-2,25
Строим график:

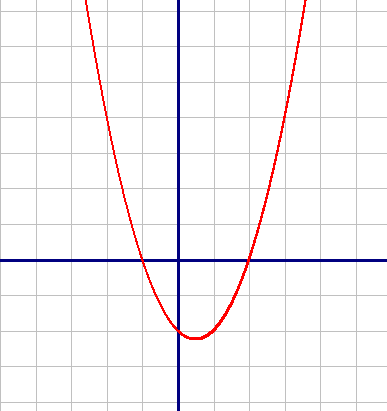
А теперь, как говорилось ранее, часть графика, которая находится под осью Х, зеркально отобразим над осью Х:

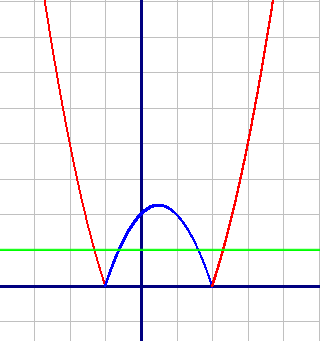
Это и будет графиком функции y=|x²-x-2|.
Очевидно, что график данной функции имеет 4 общие точки с прямой, параллельной оси абсцисс (зеленая прямая).
Ответ: 4

Поделитесь решением

Присоединяйтесь к нам...

Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас'

Другие задачи из этого раздела

Задача №24DAAC

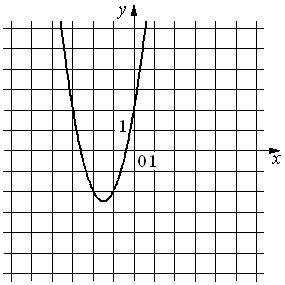На рисунке изображён график функции y=ax²+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.

УТВЕРЖДЕНИЯ	ПРОМЕЖУТКИ
А) Функция возрастает на промежутке Б) Функция убывает на промежутке	1) [-4;-2] 2) [-1;0] 3) [-2;-1] 4) [-2;0]

Задача №9F911C

Постройте график функции y=x²-6|x|-2x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.

Задача №BF2057

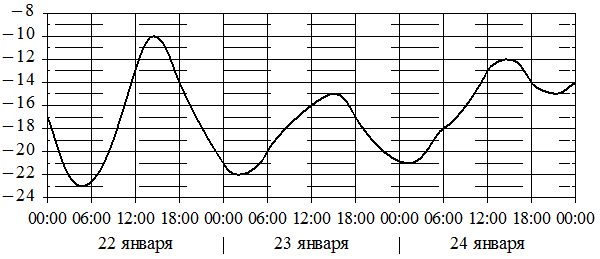На графике показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по графику наибольшую температуру воздуха 24 января. Ответ дайте в градусах Цельсия.

Задача №F80127

Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
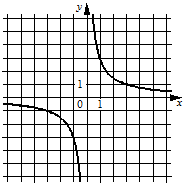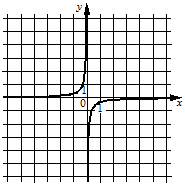А) Б) В)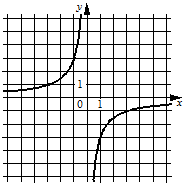
ФОРМУЛЫ
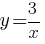1) 2) 3)
В таблице под каждой буквой укажите соответствующий номер.