Постройте график функции y=x2-3|x|-x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
В данной функции присутствует
модуль, следовательно функцию надо разложить на две подфункции, в зависимости от значения
модуля:
x2-3x-x, при x≥0
x2-3(-x)-x, при x<0
x2-4x, при x≥0
x2+2x, при x<0
Рассмотрим и построим график для каждой подфункции и объединим их.
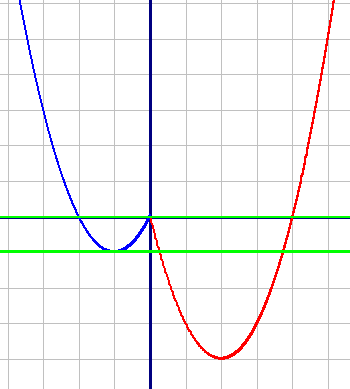1) y1=x2-4x, при x≥0 (красный график)
| X | 0 | 1 | 2 | 3 |
| Y | 0 | -3 | -4 | -3 |
| X | 0 | -1 | -2 | -3 |
| Y | 0 | -1 | 0 | 3 |
Поделитесь решением
Присоединяйтесь к нам...
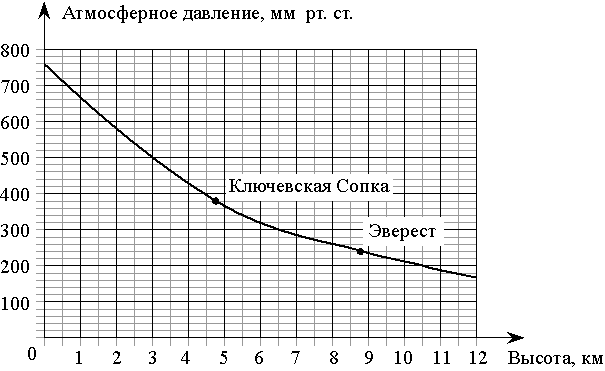На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты местности над уровнем моря (в километрах). На сколько миллиметров ртутного столба атмосферное давление на высоте Эвереста ниже атмосферного давления на высоте Ключевской Сопки?
Постройте график функции
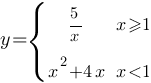и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
Постройте график функции y=x2+11x-4|x+6|+30 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Постройте график функции y=2|x-5|-x2+11x-30 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
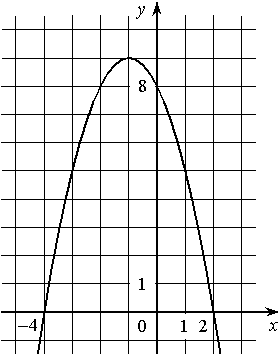На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Функция возрастает на промежутке (-∞;-1]
2) Наибольшее значение функции равно 8
3) f(-4)≠f(2)
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2024-03-30 23:13:09) Аня: Постройте график функции и определите, при каких значениях параметра c прямая имеет с графиком три общие точки.