Постройте график функции y=|x|(x-1)-3x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
В данной функции присутствуем
модуль, следовательно функцию надо разложить на две подфункции, в зависимости от значения
модуля:
y=x(x-1)-3x, при x≥0
y=(-x)(x-1)-3x, при x<0
y=x2-x-3x, при x≥0
y=-x2+x-3x, при x<0
y=x2-4x, при x≥0
y=-x2-2x, при x<0
Рассмотрим и построим график для каждой подфункции и объединим их.
1) y=x2-4x, при x≥0
Графиком данной подфункции является парабола. Ветви этой параболы направлены вверх, так как коэффициент при x2 положительный.
Найдем корни уравнения x2-4x=0
x(x-4)=0
x1=0
x-4=0
x2=4
Построим график по точкам:
| X | 0 | 1 | 2 | 3 | 4 |
| Y | 0 | -3 | -4 | -3 | 0 |
| X | 0 | -1 | -2 | -3 |
| Y | 0 | 1 | 0 | -3 |
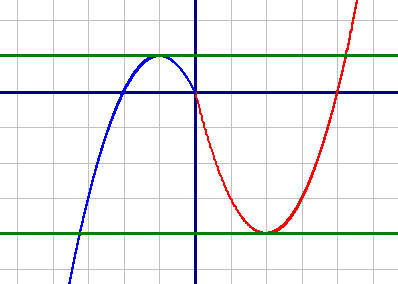Красный график: y=x2-4x, при x≥0Поделитесь решением
Присоединяйтесь к нам...
Найдите значение выражения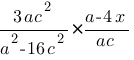 
при a=2,1, c=-0,4.
В течение августа огурцы подешевели на 20%, а затем в течение сентября подорожали на 40%. Какая цена больше: в начале августа или в конце сентября – и на сколько процентов?
Упростите выражение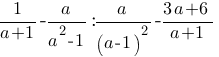 
Площадь четырёхугольника можно вычислить по формуле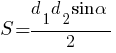 
, где d1 и d2 — длины диагоналей четырёхугольника, α — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d2,
если d1=14, sinα=1/12, a S=8,75.
Уравнение x2+px+q=0 имеет корни 5 и 9. Найдите q.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2016-10-22 20:25:22) Администратор: Павел, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2016-10-22 17:44:59) Павел: y = |7 - (x - 4)^2| + 1