Решите уравнение x(x2+2x+1)=6(x+1).
x(x2+2x+1)=6(x+1)
Заметим, что слагаемые в левой скобке представляют из себя квадрат суммы:
x(x2+2x+12)=6(x+1)
x(x+1)2=6(x+1)
x(x+1)2-6(x+1)=0
Вынесем (x+1) за общую скобку:
(x+1)(x(x+1)-6)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому рассмотрим два случая:
1) x+1=0 => x1=-1
2) x(x+1)-6=0
x2+x-6=0
Решим это квадратное уравнение через дискриминант:
D=12-4*1*(-6)=1+24=25
x2=(-1+5)/(2*1)=4/2=2
x3=(-1-5)/(2*1)=-6/2=-3
Ответ: x1=-1, x2=2, x3=-3
Поделитесь решением
Присоединяйтесь к нам...
Из пункта А в пункт В, расстояние между которыми 13 км, вышел пешеход. Одновременно с ним из В в А выехал велосипедист. Велосипедист ехал со скоростью, на 11 км/ч большей скорости пешехода, и сделал в пути получасовую остановку. Найдите скорость пешехода, если известно, что они встретились в 8 км от пункта В.
Стоимость проезда в электричке составляет 249 рублей. Школьникам предоставляется скидка 50%. Сколько рублей будет стоить проезд для 2 взрослых и 3 школьников?
Решите систему уравнений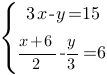 
Найдите p и постройте график функции y=x2+p, если известно, что прямая y=4x имеет с графиком ровно одну общую точку.
Найдите корень уравнения (x-10)2=(2-x)2.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: