Укажите решение неравенства
(x+1)(x-6)≤0.
1) 
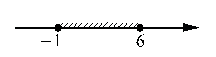
2) 
3) 
4) 
Чтобы решить это неравенство надо найти корни соответствующего уравнения:
(x+1)(x-6)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому рассмотрим два случая:
1) x+1=0 => x1=-1
2) x-6=0 => x2=6
Раскроем скобки неравенства, чтобы представить его в более удобном виде:
(x+1)(x-6)≤0
x2-6x+x-6≤0
x2-5x-6≤0
Теперь рассмотрим график нашей функции - это парабола.
Так как коэффициент при x2 равен 1, т.е. положительный, то ветви параболы направлены вверх.
Нас интересует диапазон, где наша функция меньше или равна нулю (по условию). Это означает, что график функции располагается под осью Х.
В нашем случае, график находится под осью на диапазоне от x1 до x2.
x1 и x2 - это корни, которые мы нашли ранее.
А так как неравенство нестрогое, то скобки около x1 и x2 квадратные.
[-1;6]
Ответ: 1)
Поделитесь решением
Присоединяйтесь к нам...
Рыболов проплыл на лодке от пристани некоторое расстояние вверх по течению реки, затем бросил якорь, 2 часа ловил рыбу и вернулся обратно через 5 часов от начала путешествия. На какое расстояние от пристани он отплыл, если скорость течения реки равна 4 км/ч, а собственная скорость лодки 6 км/ч?
Первую половину трассы автомобиль проехал со скоростью 84 км/ч, а вторую — со скоростью 96 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Первый рабочий за час делает на 9 деталей больше, чем второй, и заканчивает работу над заказом, состоящим из 112 деталей, на 4 часа раньше, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 1 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 20 минут назад. Найдите скорость первого бегуна, если известно, что она на 8 км/ч меньше скорости второго.
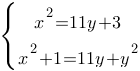
Решите уравнение x2-3x+√3-x=√3-x+10
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: