
Решите уравнение (x-5)2=(x+10)2.
Вариант 1
(x-5)2=(x+10)2
(x-5)2-(x+10)2=0
Воспользуемся формулой
разность квадратов:
((x-5)-(x+10))((x-5)+(x+10))=0
(x-5-x-10)(x-5+x+10)=0
-15(2x+5)=0 |:(-15)
2x+5=0
2x=-5
x=-2,5
Вариант 2
(x-5)2=(x+10)2
Воспользуемся формулой
квадрат суммы:
x2-2*x*5+52=x2+2*x*10+102
-10x+25=20x+100
25-100=20x+10x
-75=30x |:30
x=-2,5
Ответ: -2,5
Поделитесь решением
Присоединяйтесь к нам...
Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.
Свежие фрукты содержат 84% воды, а высушенные — 16%. Сколько требуется свежих фруктов для приготовления 44 кг высушенных фруктов?
Решите уравнение x3+2x2-x-2=0.
Решите систему уравнений 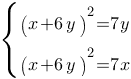
Товар на распродаже уценили на 50%, при этом он стал стоить 820 р. Сколько рублей стоил товар до распродажи?
Комментарии: