Решите уравнение x(x2+2x+1)=6(x+1).
x(x2+2x+1)=6(x+1)
Заметим, что слагаемые в левой скобке представляют из себя квадрат суммы:
x(x2+2x+12)=6(x+1)
x(x+1)2=6(x+1)
x(x+1)2-6(x+1)=0
Вынесем (x+1) за общую скобку:
(x+1)(x(x+1)-6)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому рассмотрим два случая:
1) x+1=0 => x1=-1
2) x(x+1)-6=0
x2+x-6=0
Решим это квадратное уравнение через дискриминант:
D=12-4*1*(-6)=1+24=25
x2=(-1+5)/(2*1)=4/2=2
x3=(-1-5)/(2*1)=-6/2=-3
Ответ: x1=-1, x2=2, x3=-3
Поделитесь решением
Присоединяйтесь к нам...
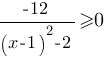
В начале года число абонентов телефонной компании «Юг» составляло 400 тыс. человек, а в конце года их стало 440 тыс. человек. На сколько процентов увеличилось за год число абонентов этой компании?
Первые 300 км автомобиль ехал со скоростью 60 км/ч, следующие 300 км — со скоростью 100 км/ч, а последние 300 км — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Городской бюджет составляет 27 млн рублей, а расходы на одну из его статей составили 10%. Сколько рублей потрачено на эту статью бюджета?
Свежие фрукты содержат 88% воды, а высушенные — 30%. Сколько требуется свежих фруктов для приготовления 6 кг высушенных фруктов?
Решите уравнение x3+5x2-x-5=0.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: