
Решите неравенство 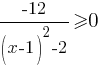
Первое: это неравенство ни при каких "х" не будет равно нулю, так как чтобы дробь была равна нулю, числитель должен быть равен нулю, а у нас он равен -12.
Значит мы можем превратить это нестрогое неравенство в строгое, ничего при этом не теряя:
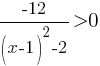
Второе: данная дробь будет больше нуля, только тогда, когда знаменатель будет меньше нуля (так как числитель отрицательный). Причем знаменатель строго меньше нуля, так как он не может быть равен нулю (на ноль делить нельзя).
Получаем неравенство:
(x-1)2-2<0 - его и надо решить.
Раскроем скобки по формуле
квадрат разности:
x2-2*x*1+12-2<0
x2-2x+1-2<0
x2-2x-1<0
Решим квадратное уравнение x2-2x-1=0 через
дискриминант
D=(-2)2-4*1*(-1)=4+4=8
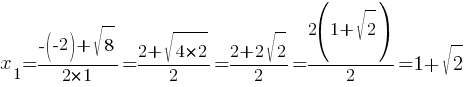
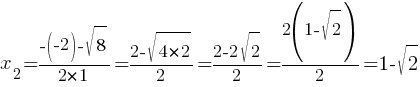
 График этой квадратичной функции - парабола. Ветви параболы направлены вверх, т.к. коэффициент "а" равен 1 (т.е. больше нуля).
График этой квадратичной функции - парабола. Ветви параболы направлены вверх, т.к. коэффициент "а" равен 1 (т.е. больше нуля).
Нас интересуют диапазон, где эта функция меньше нуля, т.е. располагается под осью Х:
(1-√2;1+√2)
Ответ: (1-√2;1+√2)
Поделитесь решением
Присоединяйтесь к нам...
При каком значении x значения выражений 10x-6 и 6x+5 равны?
Решите уравнение (x2-9)2+(x2+x-6)2=0
В начале года число абонентов телефонной компании «Север» составляло 200 тыс. человек, а в конце года их стало 250 тыс. человек. На сколько процентов увеличилось за год число абонентов этой компании?
Магазин делает пенсионерам скидку на определённое количество процентов от стоимости покупки. Батон хлеба стоит в магазине 15 рублей, а пенсионер заплатил за него 13 рублей 80 копеек. Сколько процентов составляет скидка для пенсионера?
Плата за телефон составляет 310 рублей в месяц. В следующем году она увеличится на 13%. Сколько рублей придётся платить ежемесячно за телефон в следующем году?
Комментарии: