
При каких положительных значениях k прямая y=kx-4 имеет с параболой y=x2-3x ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
Чтобы найти общую точку двух графиков, надо найти решение системы, составленное из уравнений этих графиков:
 y=kx-4
y=kx-4
y=x2-3x
kx-4=x2-3x
0=x2-3x-kx+4
0=x2-x(3+k)+4
Это квадратное уравнение должно иметь только один корень, т.к. по условию, графики пересекаются только в одной точке. Следовательно, дискриминант должен быть равен нулю.
D=(-(3+k))2-4*1*4=(3+k)2-16=0
Раскроем скобку, используя формулу квадрат суммы:
32+2*3*k+k2-16=0
k2+6k-7=0
Это тоже квадратное уравнение, и его тоже будем решать через дискриминант:
D=62-4*1*(-7)=36+28=64
k1=(-6+8)/(2*1)=2/2=1
k2=(-6-8)/(2*1)=-14/2=-7
Напомню, что мы нашли такие k, при которых графики изначальных функций имеют только одну одну общуу точку.
По условию задачи нас интересуют только положительные k, т.е. k=1.
Подставляем это значение k в решение первоначально системы уравнений (мы остановились на моменте 0=x2-x(3+k)+4).
0=x2-x(3+1)+4
0=x2-4x+4
0=x2-4x+22
Для быстроты решения применим формулу квадрат разности:
0=(x-2)2
x=2 - это координата х точки пересечения.
Чтобы найти координату y, надо подставить это значение x и полученное значение k в любое из уравнений. Проще подставить в уравнение прямой:
y=kx-4=1*2-4=2-4=-2 - это координата "y" точки пересечения.
Получаем: координаты точки пересечения графиков (2;-2).
 Построим графики по точкам:
Построим графики по точкам:
y=kx-4=x-4 (Красный график)
| X | 1 | 2 | 3 |
| Y | -3 | -2 | -1 |
| X | 0 | 1 | 2 | 3 |
| Y | 0 | -2 | -2 | 0 |
Поделитесь решением
Присоединяйтесь к нам...
Одно из чисел √40, √46, √53, √58 отмечено на прямой точкой A.
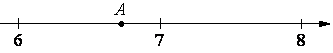
Какое это число?
1) √40
2) √46
3) √53
4) √58
На координатной прямой отмечено число a.

Из следующих утверждений выберите верное.
1) (a-6)2>1
2) (a-5)2<1
3) a2<25
4) a2>36
При каких положительных значениях k прямая y=kx-4 имеет с параболой y=x2-3x ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
Укажите решение системы неравенств
 x>-1
x>-1
3-x>0
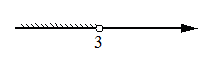
1) 
2) 
3) система не имеет решений
4) 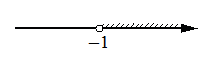
На координатной прямой отмечено число a.

Из следующих утверждений выберите верное.
1) (a-6)2>1
2) (a-7)2>1
3) a2>36
4) a2>49
Комментарии: