
Первый рабочий за час делает на 10 деталей больше, чем второй, и выполняет заказ, состоящий из 60 деталей, на 3 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
Пусть х - количество деталей, которое делает второй рабочий за час.
Тогда х+10 - количество деталей, которое делает первый рабочий за час.
t - количество часов, затраченное первым рабочим на выполнение заказа.
Тогда t+3 - количество часов, затраченное вторым рабочим на выполнение заказа.
Получаем систему:
 60=(x+10)t
60=(x+10)t
60=x(t+3)
(x+10)t=x(t+3)
xt+10t=xt+3x
10t=3x
t=3x/10=0,3x
В первое уравнение системы вместо t подставляем 0,3x (т.к. они равны):
60=(x+10)0,3x
0,3x2+10*0,3x-60=0
0,3x2+3x-60=0
Решим это квадратное уравнение через дискриминант:
D=32-4*0,3*(-60)=9+72=81
x1=(-3+9)/(2*0,3)=6/0,6=10
x2=(-3-9)/(2*0,3)=-12/0,6=-20
Отрицательным количество деталей быть не может, следовательно, ответ 10.
Ответ: 10
Поделитесь решением
Присоединяйтесь к нам...
Решите уравнение (x-3)2(x-4)=2(x-3).
Решите уравнение (4x-8)2(x-8)=(4x-8)(x-8)2.
Решите уравнение x4=(x-2)2.
На каком рисунке изображено множество решений системы неравенств
 x+3≥-2,
x+3≥-2,
x+1,1≥0?
1) 
2) 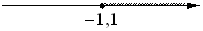
3) 
4) 
На каком рисунке изображено множество решений неравенства
3-4x>11-8(x-2)?
1) 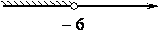
2) 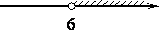
3) 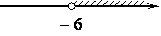
4) 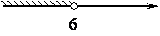
Комментарии: