Первый рабочий за час делает на 9 деталей больше, чем второй, и заканчивает работу над заказом, состоящим из 112 деталей, на 4 часа раньше, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
Пусть х - количество деталей, которое делает второй рабочий за час.
Тогда х+9 - количество деталей, которое делает первый рабочий за час.
t - количество часов, затраченное первым рабочим на выполнение заказа.
Тогда t+4 - количество часов, затраченное вторым рабочим на выполнение заказа.
Получаем систему:
112=(x+9)t
112=x(t+4)
112/(x+9)=t
112=xt+4x
112/(x+9)=t
112=x*112/(x+9)+4x
112/(x+9)=t
112=x*112/(x+9)+4x(x+9)/(x+9)
112/(x+9)=t
112=(112x+4x2+36x)/(x+9)
112/(x+9)=t
112(x+9)=148x+4x2 |:4
112/(x+9)=t
28(x+9)=37x+x2
112/(x+9)=t
28x+252=37x+x2
112/(x+9)=t
0=x2+9x-252
Решим это
квадратное уравнение:
D=92-4*1*(-252)=81+1008=1089
x1=(-9+33)/(2*1)=12
x2=(-9-33)/(2*1)=-21
Отрицательным количество деталей быть не может.
Ответ: 12
Поделитесь решением
Присоединяйтесь к нам...
Найдите корни уравнения x2+3x=18.
Решите систему неравенств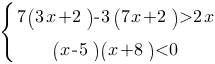 
Решите уравнение x3+2x2-x-2=0.
Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 57 км/ч, а вторую половину пути проехал со скоростью на 38 км/ч больше скорости первого, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста.
Найдите наибольшее значение x, удовлетворяющее системе неравенств
Хочу получать новые решения
Ни какого спама
Автор: Таська
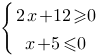
Комментарии: