
Решите неравенство 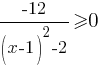
Первое: это неравенство ни при каких "х" не будет равно нулю, так как чтобы дробь была равна нулю, числитель должен быть равен нулю, а у нас он равен -12.
Значит мы можем превратить это нестрогое неравенство в строгое, ничего при этом не теряя:
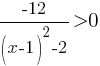
Второе: данная дробь будет больше нуля, только тогда, когда знаменатель будет меньше нуля (так как числитель отрицательный). Причем знаменатель строго меньше нуля, так как он не может быть равен нулю (на ноль делить нельзя).
Получаем неравенство:
(x-1)2-2<0 - его и надо решить.
Раскроем скобки по формуле
квадрат разности:
x2-2*x*1+12-2<0
x2-2x+1-2<0
x2-2x-1<0
Решим квадратное уравнение x2-2x-1=0 через
дискриминант
D=(-2)2-4*1*(-1)=4+4=8
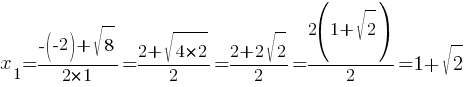
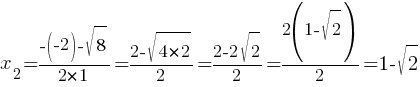
 График этой квадратичной функции - парабола. Ветви параболы направлены вверх, т.к. коэффициент "а" равен 1 (т.е. больше нуля).
График этой квадратичной функции - парабола. Ветви параболы направлены вверх, т.к. коэффициент "а" равен 1 (т.е. больше нуля).
Нас интересуют диапазон, где эта функция меньше нуля, т.е. располагается под осью Х:
(1-√2;1+√2)
Ответ: (1-√2;1+√2)
Поделитесь решением
Присоединяйтесь к нам...
Найдите корень уравнения 8+7x=9x+4.
Решите уравнение (4x-8)2(x-8)=(4x-8)(x-8)2.
Расстояние между двумя пристанями по реке равно 24 км. Моторная лодка прошла от одной пристани до другой, сделала стоянку на 1 ч 40 мин и вернулась обратно. Всё путешествие заняло 6 целых и 2/3 ч. Найдите скорость течения реки, если известно, что скорость моторной лодки в стоячей воде равна 10 км/ч.
Решите уравнение x3+2x2-x-2=0.
Укажите решение системы неравенств
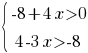
1) нет решений
2) (-∞;4)
3) (2;+∞)
4) (2;4)
Комментарии: