Какое наименьшее число последовательных натуральных чисел, начиная с 1, нужно сложить, чтобы получившаяся сумма была больше 378?
Последовательные натуральные числа - это 1, 2, 3, и т.д.
Такая последовательность является
арифметической прогрессией с a1=1 и разностью d=1.
Нам нужно найти такое наименьшее n, что сумма первых n членов (Sn) будет больше 378.
Воспользуемся формулой суммы:
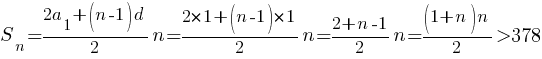
(1+n)n>756
n+n2>756
n2+n-756>0
Чтобы решить это неравенство, найдем корни соответствующего
квадратного уравнения через
дискриминант:
n2+n-756=0
D=12-4*1*(-756)=1+3024=3025
n1=(-1+55)/(2*1)=54/2=27
n1=(-1-55)/(2*1)=-56/2=-28
График квадратичной функции - парабола, так как коэффициен "а" равен 1, т.е. положителен, то ветви направлены вверх.
n2+n-756 будет больше нуля на диапазонах, где график выше оси Х, в данном случае:
n∈(-∞;-28)∪(27;+∞)
Для ответа надо выбрать наименьший n, но n, естественно, должент быть натульным, т.е. целым и положительным.
27 - не подходит, так как это число исключено из диапазона, следовательно n=28.
Ответ: 28
Поделитесь решением
Присоединяйтесь к нам...
Какое из данных ниже чисел является значением выражения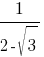 
?
1) -2-√3
2) √3-2
3) 2-√3
4) 2+√3
Постройте график функции y=|x|(x+1)-6x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
В течение августа помидоры подешевели на 50%, а затем в течение сентября подорожали на 70%. Какая цена меньше: в начале августа или в конце сентября – и на сколько процентов?
Какое из данных ниже чисел является значением выражения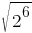 
?
1) 32
2) 16
3) 1/8
4) 8
Постройте график функции y=|x|(x-1)-2x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: