
Решите уравнение (x-1)4-2(x-1)2-3=0.
Введем обозначение:
t=(x-1)2
Тогда получаем уравнение:
t2-2t-3=0
Решим это квадратное уравнение через
дискриминант:
D=(-2)2-4*1*(-3)=4+12=16
t1=(-(-2)+4)/(2*1)=(2+4)/2=3
t2=(-(-2)-4)/(2*1)=(2-4)/2=-1
Теперь найдем "х" из параметра "t", для этого по очереди подставим оба значения "t":
1) t=3
(x-1)2=3
Можно пойти по быстрому пути решения этого уравнения:
Извлечем квадратный корень из правой и левой частей, получим:
x-1=±√3
x1=1+√3
x2=1-√3
Для тех, что не понял этот метод, пойдем по пути решения через дискриминант.
Для этого раскроем скобку (x-1)2 по формуле
квадрат разности, получаем:
x2-2*x*1+1=3
x2-2x+1-3=0
x2-2x-2=0
D=(-2)2-4*1*(-2)=4+8=12
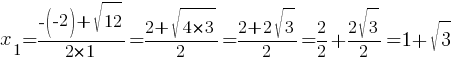
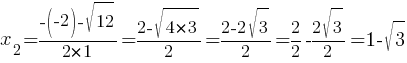
Естественно, мы получили тот же результат.
2) t=-1
(x-1)2=-1
Это уравнение не имеет решений, так как квадрат любого числа дает положительный результат и никак не может равняться -1.
Ответ: x1=1+√3, x2=1-√3
Поделитесь решением
Присоединяйтесь к нам...
Первая труба пропускает на 3 литра воды в минуту меньше, чем вторая труба. Сколько литров воды в минуту пропускает вторая труба, если резервуар объёмом 260 литров она заполняет на 6 минут быстрее, чем первая труба?
Укажите неравенство, решение которого изображено на рисунке.

1) x2-49>0
2) x2-49<0
3) x2+49<0
4) x2+49>0
Решите систему уравнений 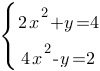
Решите уравнение 2x2+14x=0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Расстояние между пристанями А и В равно 126 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот проплыл 36 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4 км/ч.
Комментарии: