
Решите систему уравнений 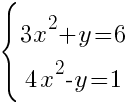
Одним из способов решения систем уравнений является сложение (или вычитание) уравнений. Этот метод надо применять в случаях, когда в результате сложения (или вычитания) в итоговом уравнении остается только одна неизвестная.
В данном случае можно применить этот способ, сложим эти уравнения:
(3x2+y)+(4x2-y)=6+1
3x2+y+4x2-y=7
7x2=7
x2=1
x2-1=0
Воспользуемся формулой разность квадратов:
x2-12=0
(x-1)(x+1)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому:
1) x-1=0 => x1=1
2) x+1=0 => x2=-1
Теперь надо найти вторую неизвестную, для этого подставляем значения "х" в любое из уравнений системы (например в первое). Так как у нас два значения "х", то это действие надо проделать для каждого значения "х":
1) Когда x=1.
3x2+y=6
3*12+y=6
3+y=6
y=6-3
y1=3
Первое решение системы (1;3).
2) Когда x=-1.
3*(-1)2+y=6
3*1+y=6
y=6-3
y2=3
Второе решение системы (-1;3).
Ответ: (1;3) и (-1;3)
Поделитесь решением
Присоединяйтесь к нам...
Решите систему неравенств 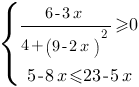
Рыболов проплыл на лодке от пристани некоторое расстояние вверх по течению реки, затем бросил якорь, 2 часа ловил рыбу и вернулся обратно через 6 часов от начала путешествия. На какое расстояние от пристани он отплыл, если скорость течения реки равна 3 км/ч, а собственная скорость лодки 6 км/ч?
Решите уравнение -3x2-14x-7=(x-1)2.
Решите систему уравнений 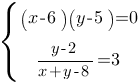
Теплоход проходит по течению реки до пункта назначения 165 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 5 часов, а в пункт отправления теплоход возвращается через 18 часов после отплытия из него.
Комментарии: