Решите уравнение x(x2+6x+9)=4(x+3).
Если внимательно посмотреть на уравнение, то можно заметить, что скобка в левой части представляет из себя квадрат суммы:
x(x2+6x+32)=4(x+3)
x(x+3)2=4(x+3)
x(x+3)2-4(x+3)=0
Вынесем за общую скобку (x+3):
(x+3)(x(x+3)-4)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому приравняем каждую скобку к нулю и найдем решения:
1) x+3=0 => x1=-3
2) x(x+3)-4=0
x2+3x-4=0
Решим это квадратное уравнение через дискриминант:
D=32-4*1*(-4)=9+16=25
x2=(-3+5)/(2*1)=2/2=1
x3=(-3-5)/(2*1)=-8/2=-4
Ответ: x1=-3, x2=1, x3=-4
Поделитесь решением
Присоединяйтесь к нам...
Найдите корень уравнения (x-10)2=(2-x)2.
Решите уравнение x2=5x.
Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Решите систему уравнений
Укажите решение неравенства 7x-x2<0.
1) 
2) 
3) 
4) 
На координатной прямой отмечено число a.
Найдите наименьшее из чисел a2, a3, a4.
1) a2
2) a3
3) a4
4) не хватает данных для ответа
Хочу получать новые решения
Ни какого спама
Автор: Таська
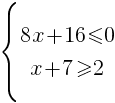
Комментарии: