Решите неравенство 2x2+x<0.
Для решения неравенства найдем корни уравнения 2x2+x=0
Можно это квадратное уравнение решить через дискриминант, но в данном случае легче решить по другому:
Выносим за скобки х:
x(2x+1)=0
Произведение равняется нулю, когда один из множителей равен нулю, поэтому рассмотрим два варианта:
1) x1=0
2) 2x+1=0
2x=-1
x2=-0,5
График функции 2x2+x представляет из себя параболу. Коэффициен "а" равен 2, т.е. больше нуля, поэтому ветви параболы направлены вверх, как на рисунке. График пересекает ось Х в точках x1 и x2.
2x2+x меньше нуля, когда график располагается ниже оси Х, т.е. на диапазоне (-0,5;0)
Ответ: (-0,5;0)
Поделитесь решением
Присоединяйтесь к нам...
Известно, что число m отрицательное. На каком из рисунков точки с координатами 0, m, 2m, m2 расположены на координатной прямой в правильном порядке?
1) 
2) 
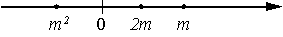
3) 
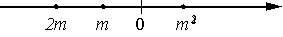
4) 
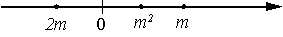
Государству принадлежит 60% акций предприятия, остальные акции принадлежат частным лицам. Общая прибыль предприятия после уплаты налогов за год составила 70 млн руб. Какая сумма (в рублях) из этой прибыли должна пойти на выплату частным акционерам?
Найдите наибольшее значение x, удовлетворяющее системе неравенств
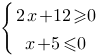
Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого автомобилиста на 11 км/ч, а вторую половину пути проехал со скоростью 66 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 40 км/ч.
Найдите корень уравнения (x-10)2=(2-x)2.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: