Решите систему уравнений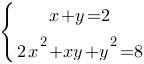 
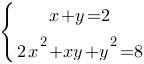
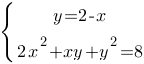
Подставим значение "y" из первого уравнения во второе:
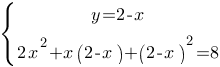
Применим формулу разность квадратов для раскрытия последней скобки:
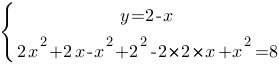
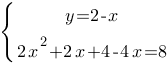
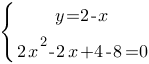
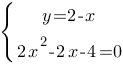
Разделим левую и правую части второго уравнения на 2, чтобы сократить коэффициенты и, тем самым, облегчить арифметические вычисления:
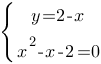
Решим
квадратное уравнение x2-x-2=0 через
дискриминант:
D=(-1)2-4*1*(-2)=1+8=9
x1=(-(-1)+3)/(2*1)=(1+3)/2=4/2=2
x2=(-(-1)-3)/(2*1)=(1-3)/2=-2/2=-1
Подставим в первое уравнение сначала первое значение x, а потом второе. В результате мы получим две пары чисел, т.е. два ответа:
1) При x=2: y=2-2 => y1=0
2) При x=-1: y=2-(-1)=2+1 => y2=3
Ответ: (2;0) и (-1;3)
Поделитесь решением
Присоединяйтесь к нам...
Туристы проплыли на лодке от лагеря некоторое расстояние вверх по течению реки, затем причалили к берегу и, погуляв 3 часа, вернулись обратно через 5 часов от начала путешествия. На какое расстояние от лагеря они отплыли, если скорость течения реки равна 2 км/ч, а собственная скорость лодки 8 км/ч?
Городской бюджет составляет 76 млн рублей, а расходы на одну из его статей составили 20%. Сколько рублей потрачено на эту статью бюджета?
Найдите корень уравнения 8+7x=9x+4.
Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 51 минуту, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 251 км, скорость первого велосипедиста равна 10 км/ч, скорость второго — 20 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого автомобилиста на 11 км/ч, а вторую половину пути проехал со скоростью 66 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 40 км/ч.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2016-10-15 15:12:49) Администратор: Tatyana, спасибо большое. Исправлено.
(2016-10-15 14:42:53) Tatyana : Корни квадратного уравнения x^2-x-2=0 (-1;2), а не (1;-2).