Решите уравнение x3+5x2=9x+45.
x3+5x2=9x+45
x3+5x2-(9x+45)=0
x2(x+5)-9(x+5)=0
Вынесем (x+5) за общую скобку:
(x+5)(x2-9)=0
(x+5)(x2-32)=0
(x+5)
(x-3)(x+3)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому рассмотрим три варианта:
1) x+5=0 => x1=-5
2) x-3=0 => x2=3
3) x+3=0 => x3=-3
Ответ: x1=-5, x2=3, x3=-3
Поделитесь решением
Присоединяйтесь к нам...
Укажите решение системы неравенств
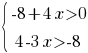
1) нет решений
2) (-∞;4)
3) (2;+∞)
4) (2;4)
Решите уравнение 7x2=42x.
Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Три бригады изготовили вместе 246 деталей. Известно, что вторая бригада изготовила деталей в 5 раз больше, чем первая и на 15 деталей меньше, чем третья. На сколько деталей больше изготовила третья бригада, чем первая.
Игорь и Паша красят забор за 20 часов. Паша и Володя красят этот же забор за 24 часа, а Володя и Игорь — за 30 часов. За сколько минут мальчики покрасят забор, работая втроём?
Решите систему уравнений 
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: