Выписаны первые несколько членов арифметической прогрессии: -6; -3; 0; … Найдите сумму первых десяти её членов.
Чтобы найти сумму
арифметической прогрессии у нас есть
две формулы.
a10 мы не знаем, поэтому воспользуемся второй формулой. Для этого найдем d - разность прогрессии.
d=a2-a1=-3-(-6)=-3+6=3.
Подставляем все в формулу:
Sn=n*(2a1+(n-1)d)/2
S10=10*(2*(-6)+(10-1)*3)/2=5*(-12+9*3)=5*(-12+27)=5*15=75
Ответ: 75
Поделитесь решением
Присоединяйтесь к нам...
Дана арифметическая прогрессия (an), разность которой равна -5,3, a1=-7,7. Найдите a7.
Выписаны первые несколько членов арифметической прогрессии: 1, 3, 5, … Найдите её одиннадцатый член.
Выписаны первые несколько членов арифметической прогрессии: 4; 7; 10; … Найдите сумму первых шестидесяти пяти её членов.
Последовательность (bn) задана условиями: b1=4,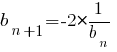 
Найдите b3.
Записаны первые три члена арифметической прогрессии: -6; 1; 8. Какое число стоит в этой арифметической прогрессии на 51-м месте?
Хочу получать новые решения
Ни какого спама
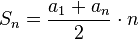, где a1 - первый член прогрессии, an - член с номером n, n — количество суммируемых членов.
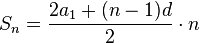, где a1 — первый член прогрессии, d — разность прогрессии, n — количество суммируемых членов. 
Автор: Таська
Комментарии: