Какое наибольшее число последовательных натуральных чисел, начиная с 1, можно сложить, чтобы получившаяся сумма была меньше 561?
Иными словами, 1+2+3+4+...+n<561. Чему равен максимальный n?
Это
арифметическая прогрессия, разность прогрессии d=1, используем
формулу суммы:
Sn=(2*1+(n-1)*1)*n/2
Эта сумма должна быть меньше 561.
(2*1+(n-1)*1)*n/2<561
(2+n-1)n<1122
n2+n-1122<0
Решим это неравенство,
решив сначала уравнение n2+n-1122=0
D=12-4*1*(-1122)=1+4488=4489
n1=(-1+67)/(2*1)=66/2=33
n2=(-1-67)/(2*1)=-68/2=-34
Т.е. n∈(-34;33), заметьте крайние точки не включаются.
nmax=32
Ответ: 32
Поделитесь решением
Присоединяйтесь к нам...
За 20 минут велосипедист проехал 7 километров. Сколько километров он проедет за t минут, если будет ехать с той же скоростью? Запишите соответствующее выражение.
Сколько целых чисел расположено между √13 и √130?
Решите систему уравнений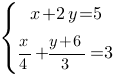 
Имеется два сплава с разным содержанием золота. В первом сплаве содержится 35% золота, а во втором – 60%. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 40% золота?
Найдите значение выражения: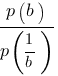
, если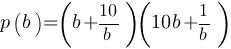 
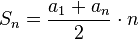Хочу получать новые решения
Ни какого спама
, где a1 - первый член прогрессии, an - член с номером n, n — количество суммируемых членов.
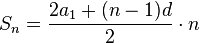, где a1 — первый член прогрессии, d — разность прогрессии, n — количество суммируемых членов. 
Автор: Таська
Комментарии: