
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ115 –Η–Ζ 1087 |
–ö–Α–Κ–Η–Β –Η–Ζ –¥–Α–Ϋ–Ϋ―΄―Ö ―É―²–≤–Β―Ä–Ε–¥–Β–Ϋ–Η–Ι –≤–Β―Ä–Ϋ―΄? –½–Α–Ω–Η―à–Η―²–Β –Η―Ö –Ϋ–Ψ–Φ–Β―Ä–Α.
1) –ß–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ―É, –Ϋ–Β –Μ–Β–Ε–Α―â―É―é –Ϋ–Α –¥–Α–Ϋ–Ϋ–Ψ–Ι –Ω―Ä―è–Φ–Ψ–Ι, –Φ–Ψ–Ε–Ϋ–Ψ –Ω―Ä–Ψ–≤–Β―¹―²–Η –Ω―Ä―è–Φ―É―é, –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ―É―é ―ç―²–Ψ–Ι –Ω―Ä―è–Φ–Ψ–Ι.
2) –Δ―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ―¹–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ–Α–Φ–Η 1, 2, 4 ―¹―É―â–Β―¹―²–≤―É–Β―².
3) –ï―¹–Μ–Η –≤ ―Ä–Ψ–Φ–±–Β –Ψ–¥–Η–Ϋ –Η–Ζ ―É–≥–Μ–Ψ–≤ ―Ä–Α–≤–Β–Ϋ
90¬Α, ―²–Ψ ―²–Α–Κ–Ψ–Ι ―Ä–Ψ–Φ–± βÄî –Κ–≤–Α–¥―Ä–Α―².
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ –Κ–Α–Ε–¥–Ψ–Β ―É―²–≤–Β―Ä–Ε–¥–Β–Ϋ–Η–Β.
1) "–ß–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ―É, –Ϋ–Β –Μ–Β–Ε–Α―â―É―é –Ϋ–Α –¥–Α–Ϋ–Ϋ–Ψ–Ι –Ω―Ä―è–Φ–Ψ–Ι, –Φ–Ψ–Ε–Ϋ–Ψ –Ω―Ä–Ψ–≤–Β―¹―²–Η –Ω―Ä―è–Φ―É―é, –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ―É―é ―ç―²–Ψ–Ι –Ω―Ä―è–Φ–Ψ–Ι", ―ç―²–Ψ ―É―²–≤–Β―Ä–Ε–¥–Β–Ϋ–Η–Β –≤–Β―Ä–Ϋ–Ψ –Ω–Ψ
―¹–≤–Ψ–Ι―¹―²–≤―É –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ―΄―Ö –Ω―Ä―è–Φ―΄―Ö.
2) "–Δ―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ―¹–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ–Α–Φ–Η 1, 2, 4 ―¹―É―â–Β―¹―²–≤―É–Β―²", ―ç―²–Ψ ―É―²–≤–Β―Ä–Ε–¥–Β–Ϋ–Η–Β –Ϋ–Β–≤–Β―Ä–Ϋ–Ψ,―².–Κ. –¥–Μ–Η–Ϋ–Α –Ψ–¥–Ϋ–Ψ–Ι –Η–Ζ ―¹―²–Ψ―Ä–Ψ–Ϋ –Ϋ–Β –Φ–Ψ–Ε–Β―² –±―΄―²―¨ –±–Ψ–Μ―¨―à–Β ―¹―É–Φ–Φ―΄ –¥–Μ–Η–Ϋ –¥–≤―É―Ö –¥―Ä―É–≥–Η―Ö ―¹―²–Ψ―Ä–Ψ–Ϋ (–Α 4>1+2).
3) "–ï―¹–Μ–Η –≤
―Ä–Ψ–Φ–±–Β –Ψ–¥–Η–Ϋ –Η–Ζ ―É–≥–Μ–Ψ–≤ ―Ä–Α–≤–Β–Ϋ
90¬Α, ―²–Ψ ―²–Α–Κ–Ψ–Ι ―Ä–Ψ–Φ–± βÄî –Κ–≤–Α–¥―Ä–Α―²". –ß―²–Ψ–±―΄ ―Ä–Ψ–Φ–± –±―΄–Μ –Κ–≤–Α–¥―Ä–Α―²–Ψ–Φ, –Ϋ–Β–Ψ–±―Ö–Ψ–¥–Η–Φ–Ψ, ―΅―²–Ψ–±―΄ –≤―¹–Β 4 ―É–≥–Μ–Α –±―΄–Μ–Η ―Ä–Α–≤–Ϋ―΄ 90¬Α.
–Δ.–Κ.
―Ä–Ψ–Φ–± - ―΅–Α―¹―²–Ϋ―΄–Ι ―¹–Μ―É―΅–Α–Ι
–Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α, ―²–Ψ –Κ –Ϋ–Β–Φ―É –Η –Ω―Ä–Η–Φ–Β–Ϋ–Η–Φ―΄ –≤―¹–Β
―¹–≤–Ψ–Ι―¹―²–≤–Α –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α, ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ (–Ω–Ψ
―¹–≤–Ψ–Ι―¹―²–≤―É –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α), –Ω―Ä–Ψ―²–Η–≤–Ψ–Ω–Ψ–Μ–Ψ–Ε–Ϋ―΄–Ι –Ω―Ä―è–Φ–Ψ–Φ―É ―É–≥–Μ―É, ―É–≥–Ψ–Μ ―²–Ψ–Ε–Β ―Ä–Α–≤–Β–Ϋ 90¬Α.
–î―Ä―É–≥–Η–Β –¥–≤–Α ―É–≥–Μ–Α –Ω–Ψ ―²–Ψ–Φ―É –Ε–Β ―¹–≤–Ψ–Ι―¹―²–≤―É ―Ä–Α–≤–Ϋ―΄ –¥―Ä―É–≥ –¥―Ä―É–≥―É.
–Γ―É–Φ–Φ–Α ―É–≥–Μ–Ψ–≤ –Φ–Ϋ–Ψ–≥–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α –≤―΄―΅–Η―¹–Μ―è–Β―²―¹―è –Ω–Ψ ―³–Ψ―Ä–Φ―É–Μ–Β (n-2)*180¬Α, –≥–¥–Β n - –Κ–Ψ–Μ–Η―΅–Β―¹―²–≤–Ψ ―É–≥–Μ–Ψ–≤. –£ –Ϋ–Α―à–Β–Φ ―¹–Μ―É―΅–Α–Β, ―É–≥–Μ–Ψ–≤ - 4. –Δ–Ψ–≥–¥–Α ―¹―É–Φ–Φ–Α ―É–≥–Μ–Ψ–≤ ―Ä–Α–≤–Ϋ–Α (4-2)*180¬Α=360¬Α.
–Δ–Ψ–≥–¥–Α –Ω–Ψ–Μ―É―΅–Α–Β―²―¹―è, ―΅―²–Ψ ―¹―É–Φ–Φ–Α –¥–≤―É―Ö –Ϋ–Β–Η–Ζ–≤–Β―¹―²–Ϋ―΄―Ö ―É–≥–Μ–Ψ–≤ ―Ä–Α–≤–Ϋ–Α 360¬Α-90¬Α-90¬Α=180¬Α. –ê ―²–Α–Κ –Κ–Α–Κ –Ψ–Ϋ–Η ―Ä–Α–≤–Ϋ―΄ –¥―Ä―É–≥ –¥―Ä―É–≥―É, ―²–Ψ –Κ–Α–Ε–¥―΄–Ι –Η–Ζ –Ϋ–Η―Ö ―Ä–Α–≤–Β–Ϋ 180¬Α/2=90¬Α.
–Δ.–Β. –Φ―΄ ―É–Ζ–Ϋ–Α–Μ–Η, ―΅―²–Ψ –≤―¹–Β ―΅–Β―²―΄―Ä–Β ―É–≥–Μ–Α ―Ä–Α–≤–Ϋ―΄ –Ω–Ψ 90¬Α, ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ ―ç―²–Ψ ―É―²–≤–Β―Ä–Ε–¥–Β–Ϋ–Η–Β –≤–Β―Ä–Ϋ–Ψ.
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
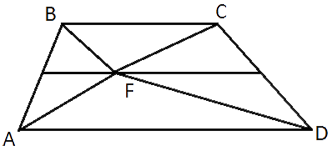 –ù–Α ―¹―Ä–Β–¥–Ϋ–Β–Ι –Μ–Η–Ϋ–Η–Η ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD ―¹ –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è–Φ–Η AD –Η BC –≤―΄–±―Ä–Α–Μ–Η –Ω―Ä–Ψ–Η–Ζ–≤–Ψ–Μ―¨–Ϋ―É―é ―²–Ψ―΅–Κ―É F. –î–Ψ–Κ–Α–Ε–Η―²–Β, ―΅―²–Ψ ―¹―É–Φ–Φ–Α –Ω–Μ–Ψ―â–Α–¥–Β–Ι ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–≤ BFC –Η AFD ―Ä–Α–≤–Ϋ–Α –Ω–Ψ–Μ–Ψ–≤–Η–Ϋ–Β –Ω–Μ–Ψ―â–Α–¥–Η ―²―Ä–Α–Ω–Β―Ü–Η–Η.
–ù–Α ―¹―Ä–Β–¥–Ϋ–Β–Ι –Μ–Η–Ϋ–Η–Η ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD ―¹ –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è–Φ–Η AD –Η BC –≤―΄–±―Ä–Α–Μ–Η –Ω―Ä–Ψ–Η–Ζ–≤–Ψ–Μ―¨–Ϋ―É―é ―²–Ψ―΅–Κ―É F. –î–Ψ–Κ–Α–Ε–Η―²–Β, ―΅―²–Ψ ―¹―É–Φ–Φ–Α –Ω–Μ–Ψ―â–Α–¥–Β–Ι ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–≤ BFC –Η AFD ―Ä–Α–≤–Ϋ–Α –Ω–Ψ–Μ–Ψ–≤–Η–Ϋ–Β –Ω–Μ–Ψ―â–Α–¥–Η ―²―Ä–Α–Ω–Β―Ü–Η–Η.
 –ë–Ψ–Κ–Ψ–≤–Α―è ―¹―²–Ψ―Ä–Ψ–Ϋ–Α ―²―Ä–Α–Ω–Β―Ü–Η–Η ―Ä–Α–≤–Ϋ–Α 5, –Α –Ψ–¥–Η–Ϋ –Η–Ζ –Ω―Ä–Η–Μ–Β–≥–Α―é―â–Η―Ö –Κ –Ϋ–Β–Ι ―É–≥–Μ–Ψ–≤ ―Ä–Α–≤–Β–Ϋ 30¬Α. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η, –Β―¹–Μ–Η –Β―ë –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è ―Ä–Α–≤–Ϋ―΄ 3 –Η 9.
–ë–Ψ–Κ–Ψ–≤–Α―è ―¹―²–Ψ―Ä–Ψ–Ϋ–Α ―²―Ä–Α–Ω–Β―Ü–Η–Η ―Ä–Α–≤–Ϋ–Α 5, –Α –Ψ–¥–Η–Ϋ –Η–Ζ –Ω―Ä–Η–Μ–Β–≥–Α―é―â–Η―Ö –Κ –Ϋ–Β–Ι ―É–≥–Μ–Ψ–≤ ―Ä–Α–≤–Β–Ϋ 30¬Α. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η, –Β―¹–Μ–Η –Β―ë –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è ―Ä–Α–≤–Ϋ―΄ 3 –Η 9.
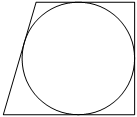 –†–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –≤–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –≤ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ―É―é ―²―Ä–Α–Ω–Β―Ü–Η―é, ―Ä–Α–≤–Β–Ϋ 18. –ù–Α–Ι–¥–Η―²–Β –≤―΄―¹–Ψ―²―É ―ç―²–Ψ–Ι ―²―Ä–Α–Ω–Β―Ü–Η–Η.
–†–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –≤–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –≤ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ―É―é ―²―Ä–Α–Ω–Β―Ü–Η―é, ―Ä–Α–≤–Β–Ϋ 18. –ù–Α–Ι–¥–Η―²–Β –≤―΄―¹–Ψ―²―É ―ç―²–Ψ–Ι ―²―Ä–Α–Ω–Β―Ü–Η–Η.
–ü–Ψ–Μ –Κ–Ψ–Φ–Ϋ–Α―²―΄, –Η–Φ–Β―é―â–Β–Ι ―³–Ψ―Ä–Φ―É –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―¹–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ–Α–Φ–Η 4 –Φ –Η 10 –Φ, ―²―Ä–Β–±―É–Β―²―¹―è –Ω–Ψ–Κ―Ä―΄―²―¨ –Ω–Α―Ä–Κ–Β―²–Ψ–Φ –Η–Ζ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ―΄―Ö –¥–Ψ―â–Β―΅–Β–Κ ―¹–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ–Α–Φ–Η 5 ―¹–Φ –Η 20 ―¹–Φ. –Γ–Κ–Ψ–Μ―¨–Κ–Ψ –Ω–Ψ―²―Ä–Β–±―É–Β―²―¹―è ―²–Α–Κ–Η―Ö –¥–Ψ―â–Β―΅–Β–Κ?
 –£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β –ê–£–Γ ―É–≥–Μ―΄ –ê –Η –Γ ―Ä–Α–≤–Ϋ―΄ 30¬Α –Η 50¬Α ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ –Φ–Β–Ε–¥―É –≤―΄―¹–Ψ―²–Ψ–Ι –£–ù –Η –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Ψ–Ι BD.
–£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β –ê–£–Γ ―É–≥–Μ―΄ –ê –Η –Γ ―Ä–Α–≤–Ϋ―΄ 30¬Α –Η 50¬Α ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ –Φ–Β–Ε–¥―É –≤―΄―¹–Ψ―²–Ψ–Ι –£–ù –Η –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Ψ–Ι BD.
–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η:
(2014-11-04 14:54:06) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –™–Α–Μ–Η–Ϋ–Α, –Ψ―΅–Β–Ϋ―¨ ―Ä–Α–¥, ―΅―²–Ψ –Ϋ–Α―à ―¹–Α–Ι―² –£–Α–Φ –Ω–Ψ–Φ–Ψ–≥!
(2014-11-04 14:44:19) –™–Α–Μ–Η–Ϋ–Α: –≤―¹―ë –≤–Β―Ä–Ϋ–Ψ ―É –Φ–Β–Ϋ―è ―¹―²–Ψ–Η―² –Ω―è―²―¨ –Ζ–Α –≤―¹–Β ―ç―²–Η –Ζ–Α–¥–Α–Ϋ–Η―è –≤ ―²–Ψ–Φ ―΅–Η―¹–Μ–Β –Η ―ç―²–Ψ!