Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны.
2) В любой четырёхугольник можно вписать окружность.
3) Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника.
Рассмотрим каждое утверждение.
1) "Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны", это утверждение верно по
свойствам углов.
2)"В любой четырёхугольник можно вписать окружность", это утверждение неверно, т.к. должны выполниться
определенные условия.
3) "Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника", это утверждение верно, по
теореме об описанной окружности.
Поделитесь решением
Присоединяйтесь к нам...
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 4 м?
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=20, DK=15, BC=12. Найдите AD.
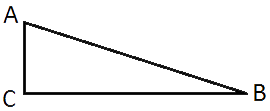Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 40 и 85.
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=6, AC=10.
Площадь прямоугольного треугольника равна 2√
Хочу получать новые решения
Ни какого спама
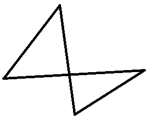(«простой»), должен быть выпуклым.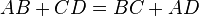
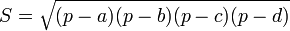
Автор: Таська
Комментарии: