
Укажите номера верных утверждений.
1) Центр вписанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Ромб не является параллелограммом.
3) Сумма острых углов прямоугольного треугольника равна 90°.
Рассмотрим каждое утверждение:
1) "Центр вписанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника". Центр
вписанной окружности любого треугольника - точка пересечения
биссектрис (по
свойству вписанной окружности). А в
равнобедренном треугольнике высота, проведенная к основанию является и
биссектрисой и медианой (
свойство). Следовательно, это утверждение верно.
2) "Ромб не является параллелограммом", это утверждение неверно, т.к. противоречит
определению ромба.
3) "Сумма острых углов прямоугольного треугольника равна 90°". В теореме о сумме углов треугольника говорится, что сумма всех углов треугольника равна 180°. В прямоугольном треугольнике один из углов равен 90°, следовательно, сумма двух оставшихся углов равна 180°-90°=90°. Т.е. это утверждение верно.
Поделитесь решением
Присоединяйтесь к нам...
В параллелограмме KLMN точка A — середина стороны LM. Известно, что KA=NA. Докажите, что данный параллелограмм — прямоугольник.
 Человек, рост которого равен 2 м, стоит на расстоянии 3,5 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).
Человек, рост которого равен 2 м, стоит на расстоянии 3,5 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).
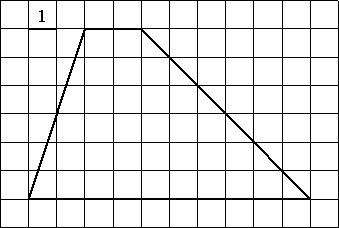 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
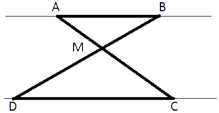 Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=16, DC=24, AC=25.
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=16, DC=24, AC=25.
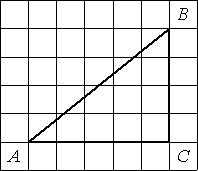 Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
 .
.
Комментарии: