
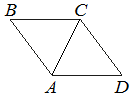
 В ромбе ABCD угол ABC равен 72°. Найдите угол ACD. Ответ дайте в градусах.
В ромбе ABCD угол ABC равен 72°. Найдите угол ACD. Ответ дайте в градусах.
Рассмотрим треугольник ABC.
AB=BC (по определению ромба).
Следовательно, треугольник ABC -
равнобедренный.
∠CAB=∠ACB (по свойству равнобедренного треугольника).
По
теореме о сумме углов треугольника:
180°=∠CAB+∠ACB+∠ABC
180°=∠ACB+∠ACB+72°
180°-72°=2*∠ACB
108°=2*∠ACB
∠ACB=54°
Рассмотрим треугольники ABC и ADC:
1) AB=BC=CD=DA (по определению ромба).
2) AC - общая сторона.
Тогда по 3-му признаку данные треугольники равны.
Следовательно:
∠ACD=∠ACB=54°
Ответ: 54
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) Медиана равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию.
2) Диагонали любого прямоугольника делят его на 4 равных треугольника.
3) Для точки, лежащей внутри круга, расстояние до центра круга меньше его радиуса.
 Точка О – центр окружности, /ACB=24° (см. рисунок). Найдите величину угла AOB (в градусах).
Точка О – центр окружности, /ACB=24° (см. рисунок). Найдите величину угла AOB (в градусах).
 Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 6.
Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 6.
 Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 7.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 7.
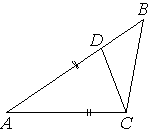 Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=19° и ∠ACB=160°. Найдите угол DCB. Ответ дайте в градусах.
Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=19° и ∠ACB=160°. Найдите угол DCB. Ответ дайте в градусах.
Комментарии: