Укажите номера верных утверждений.
1) Центры вписанной и описанной окружностей равнобедренного треугольника совпадают.
2) Существует параллелограмм, который не является прямоугольником.
3) Сумма углов тупоугольного треугольника равна 180°.
Рассмотрим каждое утверждение:
1) "Центры
вписанной и описанной окружностей
равнобедренного треугольника совпадают." - это утверждение неверно, т.к. центр вписанной окружности находится внутри треугольника, а центр описанной окружности может находиться вне треугольника (по
теореме об окружности).
2) "Существует
параллелограмм, который не является
прямоугольником." - это утверждение верно, т.к. не противоречит
определению параллелограмма.
3) "Сумма углов
тупоугольного треугольника равна 180°." - это утверждение верно, т.к. не противоречит
теореме о сумме углов треугольника.
Поделитесь решением
Присоединяйтесь к нам...
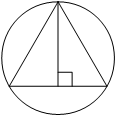Радиус окружности, описанной около равностороннего треугольника, равен 6. Найдите высоту этого треугольника.
Косинус острого угла A треугольника ABC равен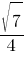 
. Найдите sinA.
Радиус окружности, описанной около квадрата, равен 48√2. Найдите радиус окружности, вписанной в этот квадрат.
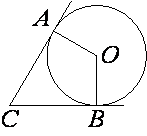В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.
В трапеции ABCD AB=CD, AC=AD и ∠ABC=95°. Найдите угол CAD. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: