
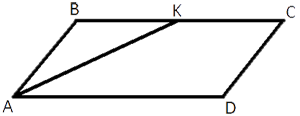 Сторона BC параллелограмма ABCD вдвое больше стороны AB.
Точка K — середина стороны BC. Докажите, что AK — биссектриса
угла BAD.
Сторона BC параллелограмма ABCD вдвое больше стороны AB.
Точка K — середина стороны BC. Докажите, что AK — биссектриса
угла BAD.
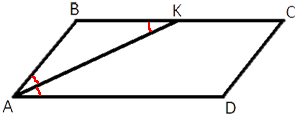 Стороны AD и BC параллельны по
определению параллелограмма.
Стороны AD и BC параллельны по
определению параллелограмма.
Тогда АК мы можем рассмотривать как секущую.
Тогда ∠DAK=∠BKA (так как они
накрест-лежащие).
ВК - вдвое меньше BC (т.к. К - середина).
AB тоже вдвое меньше BC (по условию).
Следовательно, BK=AB, т.е. треугольник ABK равнобедренный.
Тогда, по свойству равнобедренного треугольника, ∠BAK=∠BKA.
Получается, что ∠BAK=∠BKA=∠DAK.
Т.е. AK - биссектрисса.
Поделитесь решением
Присоединяйтесь к нам...
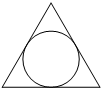 Радиус окружности, вписанной в равносторонний треугольник, равен 2√
Радиус окружности, вписанной в равносторонний треугольник, равен 2√
 Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 31.
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 31.
Какие из данных утверждений верны? Запишите их номера.
1) Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) У равностороннего треугольника есть центр симметрии.
 Катеты прямоугольного треугольника равны 4√
Катеты прямоугольного треугольника равны 4√
Стороны AC, AB, BC треугольника ABC равны 3√

Комментарии: