Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD=10. Докажите, что треугольники CBD и ADB подобны.
ABCD -
трапеция, следовательно, AD||BC.
∠CBD=∠ADB (т.к. это
накрест-лежащие углы для параллельных прямых AD и BC).
Рассмотрим отношения сторон:
BC/BD=5/10=1/2
BD/AD=10/20=1/2
Тогда по
второму признаку подобия треугольников, треугольники CBD и ADB подобны.
Поделитесь решением
Присоединяйтесь к нам...
Стороны AC, AB, BC треугольника ABC равны 3√
Проектор полностью освещает экран A высотой 50 см, расположенный на расстоянии 140 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 260 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Хорды AC и BD окружности пересекаются в точке P, BP=12, CP=15, DP=25. Найдите AP.
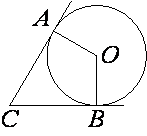В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB=20, CD=48, а расстояние от центра окружности до хорды AB равно 24.
Хочу получать новые решения
Ни какого спама
, или 
, где m - средняя линия трапеции. 
Автор: Таська
Комментарии:
(2017-03-01 23:37:56) Администратор: Таня, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправте заявку на добавление задачи, и мы ее обязательно добавим.
(2017-02-28 20:37:47) Таня: В треугольнике со сторонами 6 см,8 см и 10 проведены среднии линии.Найдите периметр треугольника ,сторонами которого являются средние линии данного треугольника .